Área do Triângulo por meio da Geometria Analítica

Vamos determinar a área de um triângulo do ponto de vista da geometria analítica. Assim, considere três pontos quaisquer,
não colineares, A (xa, ya), B (xb, yb) e C (xc, yc). Como esses pontos não são colineares, ou seja, não pertencem a uma mesma reta, eles determinam um triângulo. 

A área desse triângulo será dada por:

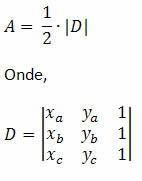
Observe que a área A será metade do módulo do determinante das coordenadas dos pontos A, B e C.

Exemplo 1. Calcule a área do triângulo cujos vértices são: A (2 , 0), B (-1 , 3) e C (0 , 6).

Resolução: Primeiro passo é calcular o determinante das coordenadas dos pontos A, B e C. então vamos lá:

Portanto, a área do triângulo de vértices A (2 , 0), B (-1 , 3) e C (0 , 6) é 6.

Exemplo 2. Determine a área do triângulo cujos vértices são: A (1, 3), B (2, 5) e C (-2,4).

Resolução: Primeiro devemos realizar o cálculo do determinante.

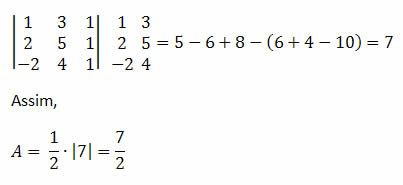
Logo área do triângulo cujos vértices são: A (1, 3), B (2, 5) e C (-2,4) é 7/2 ou 3,5.

Exemplo 3. Os pontos A (0, 0), B (0, -8) e C (x, 0) determinam um triângulo de área igual a 20. Sabendo disso encontre o valor de x.

Resolução: Sabemos que a área do triângulo de vértices A, B e C é 20. Então, substituímos na fórmula

Veja o vídeo de um exemplo: clique aqui

Exercícios:

1. Calcule a área do triângulo abaixo, em cm2, utilizando a Geometria Analítica.

A = 6 cm²

2. Calcule a área do triângulo de vértices A (2,2), B (3,0) e C (– 2, 4).

A = 3

3. Dados os pontos A (1,1) e B (10,10), qual deve ser a coordenada y do ponto C (10, y) para que a área do triângulo que tem A, B e C como vértices seja igual a 45?

y = 20

4. Calcule a coordenada x do ponto A = (x,1) e do ponto B (x,2) sabendo que as coordenadas do ponto C são (4,2), que eles não são colineares e que a área do triângulo formado por eles é igual a 3.

x = 10

Professor Claudio

30/03/2020