7 e 17 são termos equidistantes dos extremos;
9 e 15 são termos equidistantes dos extremos;
11 e 13 são termos equidistantes dos extremos.
Observe:
5 + 19 = 24 → soma dos extremos
7 + 17 = 24 → soma de dois termos equidistantes dos extremos
9 + 15 = 24 → soma de dois termos equidistantes dos extremos
11 + 13 = 24 → soma de dois termos equidistantes dos extremos
Baseada nessa ideia, existe a seguinte propriedade:
Numa PA finita, a soma de dois termos equidistantes dos extremos é igual a soma dos extremos.
Através dessa propriedade, podemos descobrir a fórmula para a soma dos n termos de uma PA:
Vamos considerar a PA finita 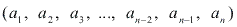 . Podemos representar por
. Podemos representar por 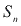 a soma dos termos dessa PA.
a soma dos termos dessa PA.
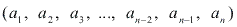 . Podemos representar por
. Podemos representar por 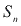 a soma dos termos dessa PA.
a soma dos termos dessa PA.
Como a soma de dois termos equidistantes dos extremos é igual a soma dos extremos, a soma da PA é dada pela soma dos extremos vezes a metade do número de termos 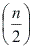 , pois em cada soma estão envolvidos dois termos.
, pois em cada soma estão envolvidos dois termos.
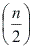 , pois em cada soma estão envolvidos dois termos.
, pois em cada soma estão envolvidos dois termos.
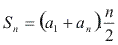
Assim, temos a fórmula da soma dos n termos de uma PA:
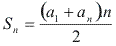
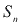 = soma dos n termos
= soma dos n termos 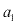 = primeiro termo
= primeiro termo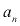 = enésimo termo
= enésimo termo
n = número de termos
Observação: Através dessa fórmula, podemos calcular a soma dos n primeiros termos de uma PA qualquer, basta determinarmos o número de termos que queremos somar.
Exemplo 1
Qual a soma dos 10 primeiros termos da PA (1, 4, 7, ...) ?
Resolução: Primeiramente, temos de descobrir qual é o 10º termo dessa PA:
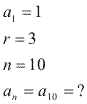
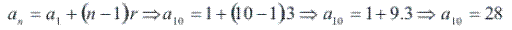
Conhecendo o valor do 10º termo, podemos calcular a soma dos 10 primeiros termos dessa PA:
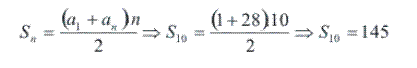
Portanto, a soma dos 10 primeiros termos da PA (1, 4, 7, ...) é 145.
Exemplo 2
A soma dos n primeiros números pares positivos de uma PA é 132. Encontre o valor de n.
Resolução: Primeiramente, vamos descobrir qual é o enésimo termo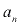 :
:
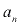 :
: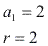
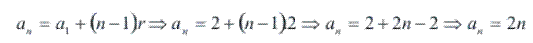
Substituindo na fórmula da soma dos termos:
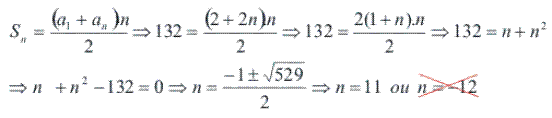
Portanto, a soma dos 11 primeiros números pares positivos é 132.
Professor Claudio
03/04/2020
Professor Claudio
03/04/2020
Fonte: https://www.somatematica.com.br/emedio/pa/pa4.php acesso em 22/03/2020

Nenhum comentário:
Postar um comentário
Em breve seu comentário será publicado.